Il teorema di Viviani

Cari lettori del Tamburo, oggi parliamo di un teorema geometrico poco noto, ma assai semplice nella formulazione: il teorema di Viviani.
Esso prende il nome da Vincenzo Viviani (1622-1703), matematico e fisico di grandissimo ingegno, a tal punto che Galileo lo reclutò come collaboratore scientifico nella sua casa ad Arcetri.
Viviani propose una sua dimostrazione del teorema nel 1659, dimostrazione che come vedremo è facilmente derivabile dalla formula dell'area di un triangolo.
Alla morte di Galileo, avvenuta nel 1642, Viviani redasse una biografia del suo mentore e cercò di curare un'edizione completa delle sue opere, tuttavia andò incontro alla dura opposizione della Chiesa, la quale offuscò la reputazione di Viviani.
Oltre a ciò, nel 1690 diede alle stampe l'edizione italiana degli Elementi di Euclide.
Ma veniamo al teorema, che cosa afferma?
Innanzitutto immaginate un triangolo equilatero e considerate un punto P situato al suo interno.
Ora da questo punto bisognerà tracciare i 3 segmenti perpendicolari ai lati.
Il teorema di Viviani enuncia che indipendentemente da dove scegliete il punto P, la somma delle distanze del punto P dai lati del triangolo sarà eguale all'altezza del triangolo!

Semplice vero? Perfetto, come si dimostra?
Sia ABC un generico triangolo equilatero, che ha altezza pari ad h e la lunghezza dei lati pari ad a.
Sia P un generico punto all'interno di ABC e siano d₁, d₂, d₃ le distanze di P dai lati.
Tracciamo, come nella figura di cui sotto, le linee che vanno da P sino ad A, B e C, andando a generare i rispettivi triangoli PAB, PBC e PCA.

Calcoliamo le aree di questi 3 piccoli triangolini:












La somma di queste 3 aree restituisce ovviamente l'area del triangolo originario ABC.
Perciò possiamo senza problemi scrivere l'uguaglianza:





Da cui




Come volevasi dimostrare!
Per chi desiderasse una dimostrazione più elegante e senza spendere alcuna parola, eccola:

Ci credete che possiamo estendere senza problemi il suddetto teorema al tetraedro regolare?
Ricordiamo che il tetraedro regolare è uno dei 5 solidi platonici ed è costituito da 4 facce uguali che sono giustappunto triangoli equilateri:

Il tetraedro non designa soltanto una figura fondamentale all'interno della geometria solida, ma si riscontra molto spesso in ambito chimico.
Giusto per citare un esempio, i silicati (i minerali più abbondanti della crosta terrestre) si basano sullo ione silicato, un tetraedro composto da uno ione silicio al centro circondato da 4 ioni ossigeno, esprimibile mediante la formula (SiO₄)^4-.
Questi tetraedri possono essere isolati o possono legarsi ad altri tetraedri, generando anelli, catene singole, catene doppie, strati o reticoli tridimensionali.

Il teorema di Viviani concernente il tetraedro regolare stabilisce quanto segue: la somma delle distanze perpendicolari di un punto P interno al tetraedro dalle 4 facce è costante ed è equivalente all'altezza del tetraedro.
Per mostrare ciò non c'è bisogno di ricorrere al calcolo di volumi.
Tracciamo invece piani paralleli alle facce del tetraedro ABCD, al fine di costruire 4 più piccoli tetraedri al suo interno che hanno un vertice comune in P e altezze d₁, d₂, d₃, d₄.

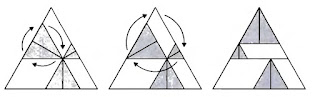
Dopodichè ruotiamo la parte più in alto del tetraedro ABCD (la quale contiene 3 piccoli tetraedri) di 120° gradi rispetto all'asse di simmetria, come viene mostrato nell'immagine che segue:

A questo punto si procede con una seconda rotazione di 120°, questa volta usando la sezione del tetraedro originario contenente i 2 tetraedri più piccoli posti in cima:

Infine, si attua un'ultima rotazione di 120° del più minuscolo e più in alto dei 4 piccoli tetraedri:

Risulta ora facile constatare che la somma delle distanze d₁, d₂, d₃ e d₄ equivale all'altezza del tetraedro ABCD di partenza! Come volevasi dimostrare!
Alcuni matematici hanno trovato la maniera di estendere il teorema di Viviani persino a problemi in cui il punto è preso fuori dal triangolo e ne hanno analizzato l'applicazione a qualsivoglia poligono regolare avente n lati.
In tal caso, la somma delle distanze dal punto interno agli n lati è equivalente a n volte l'apotema del poligono, ovvero il segmento perpendicolare condotto dal centro di un poligono a un lato.
Volendo si potrebbe proporre anche ai bambini il teorema di Viviani attraverso un'analogia surfistica.
Immaginiamo che un surfista sbarchi su un'isola che ha la forma di un triangolo equilatero e che voglia posizionare la sua capanna in modo tale che la somma delle distanze dalle coste dell'isola triangolare sia minima, poiché costui desidera fare surf da ognuna delle 3 spiagge un numero identico di volte.
Ebbene, come ormai ben sappiamo, il posizionamento della capanna in un certo punto o in qualsiasi altro dell'isola non cambia proprio niente!
A Viviani si deve anche una particolare curva, chiamata appunto curva o finestra di Viviani.
Studiata da Viviani nel 1692, essa si ottiene dall'intersezione di una sfera di raggio 2a (centrata nell'origine degli assi) con un cilindro centrato in (a, 0, 0) di raggio a.
Eccola a voi:

Alla prossima!

Questo post partecipa al Carnevale della Matematica n.91, ospitato su MaddMaths!